判断一个整数是否是2的乘方
1.题目:实现一个方法,判断一个正整数是否是2的乘方(比如 16 是 2 的 4 次方,返回 True;18 不是 2 的乘方,返回 False )。要求性能尽可能高。
解法一:
创建一个变量 Temp ,初始值是 1 。然后进入一个循环,循环中每次让Temp和目标整数比较,如果相等,则说明目标整数是 2 的乘方;如果不相等,则让 Temp 增大乘 2 ,继续循环比较。当 Temp 大于目标整数时(所以循环的判断条件是小于等于),说明目标整数不是 2 的乘方。/** * 判断整数(number)是否是2的乘方 * * @param number * @return */ public static boolean isPower2_ONE(int number) { int temp = 1; while (temp <= number) { if (temp == number) { return true; } temp = temp * 2; } return false; }
优化:
先了解一个知识点:<<(左移)乘二,>>(右移)除二具体的介绍:
的左移和右移不是循环移动,遵循下面的规则:
1.右移
右移运算用来将一个数的二进制位序列右移若干位。例如 x>>=2 ,使 x 的各二进制位右移两位,移到右端的低位被舍弃,最高位则移入原来高位的值。例如:x=00110111,则 x>>2 为 00001101 ; y=11010011 ,则 y>>2 为111101002.左移
左移运算用来将一个数的二进制位序列左移若干位。例如 x<<=2 ,使 x 的各二进制位左移两位,右边补 0 ,若x=00001111,则x<<2为00111100.最高位左移后溢出,舍弃不起作用。右移运算相当于对这个数字除2取商,左移运算相当于对这个数字乘2,而且使用左移右移实现乘法除法比使用乘法除法运算速度要快。
注意:以上等效是在不溢出的情况下进行。对于负数运算的左移是必然会溢出的
当然,如果要实现对负数的操作,由于计算机在处理负数的时候是对补码进行操作,所以除2其实是对补码的操作,因此对负数的操作需要对补码进行处理。
注意:补码运算的时候,最与最高位符号位是要保持不变的。另外,如果左移右移大于数据类型长度时候,会先取模。比如 int i ,左移 33 ,会变为左移 1 ,也就是 33%32
因此我们可以把上面循环中的乘 2 ,换成左移一位,因为左移运算符会比乘法的效率快很多。
/** * 判断整数(number)是否是2的乘方(把乘2换成左移一位) * * @param number * @return */ public static boolean isPower2_TWO(int number) { int temp = 1; while (temp <= number) { if (temp == number) { return true; } temp = temp << 1; } return false; }
虽然换成左移运算法效率会变快,可是时间复杂度还是没有变化的,也就是说本质还是没有改变。
解法二:
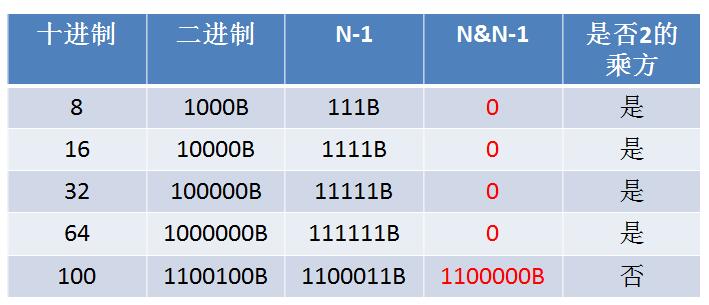
观察下面的图,我们可以发现什么规律呢?通过观察我们可以发现:
(1) 凡是2的乘方的正整数,其二进制数必然是以 1 为首位,其它位都是 0 (2) 如果给它减 1 ,(在位数相同的情况下)就会变成首位是 0 ,其它位全部是 1 的结果 (3) 0 和 1 的按位与运算结果是 0 ,因此 2 的乘方和他本身减1相与,即 N & N-1,结果必然是 0;也就是说用“位与”运算,得到的结果是0,就说明这个正整数是2的乘方所以,2 的乘方都符合一个规律,即 N&N-1 等于 0,所以直接用这个规律判断即可,但是,这个结论就一定正确吗?这只是我们通过观察部分数据得出的结果,况且我们的数据量非常的少,怎样才能保证这个结论是正确的呢?我们可以通过反证法来证明:
假设真的存在一个正整数 N,N 不是 2 的幂,但是 N 符合 N&N-1 =0。
由 N 不是 2 的幂可以推断出,N 的二进制形式并不是除了最高位是1以外,其余为全是 0 。
既然其余位不全是 0 ,那么 N-1 的结果的最高位一定不会改变,仍然是1。
既然 N-1 的最高位是 1 ,N的最高位也是 1 ,那么 N&N-1!=0,和假设矛盾。
由此证明,符合 N&N-1 =0 的正整数必然是 2 的幂。
最后我们用代码来实现:
/** * 判断整数(number)是否是2的乘方(位与运算) * * @param number * @return */ public static boolean isPower2_THREE(int number) { return (number & number - 1) == 0; } 二、求出一个正整数转换成二进制后的数字“1”的个数
题目:求出一个正整数转换成二进制后的数字“1”的个数
如: int 型数值为 80 转化成二进制形式:80 = 00000000 00000000 00000000 01010000 因此 1 的个数为 2解法一:
由上面的位运算判断 2 的乘方可以知道,n&(n-1) 可以把整数二进制的最右边的数由 1 变为 0 ,利用这个我们就可以解决这个问题了。具体实现的代码如下:
/** * 计算一个int型数值中bit-1的个数 * * @param n * @return */ public static int bitCount1(int n) { int count = 0; while (n != 0) { n = n & (n - 1); count++; } return count; }
解法二:
我们也可以通过移位来解决这题,因为整数的二进制与 1 进行 & 运算的时候,当最末位也就是最右边的一位为 1 的时候,结果就是 1 ,判断完最后一位,然后把整数的二进制右移一位,再判断,直到整数等于 0 结束循环
/** * 计算一个int型数值中bit-1的个数 * * @param n * @return */ public static int bitCount2(int n) { int count = 0; while (n > 0) { if ((n & 1) == 1) {// 如果最右边的值是1 count++; } n >>= 1; // 向右一位 } return count; } 可是这种做法不是太好,因为 Java 中 int 占 4 个字节,一共 32 位,那么就是说,要循环 32 次才能结束
解法三:
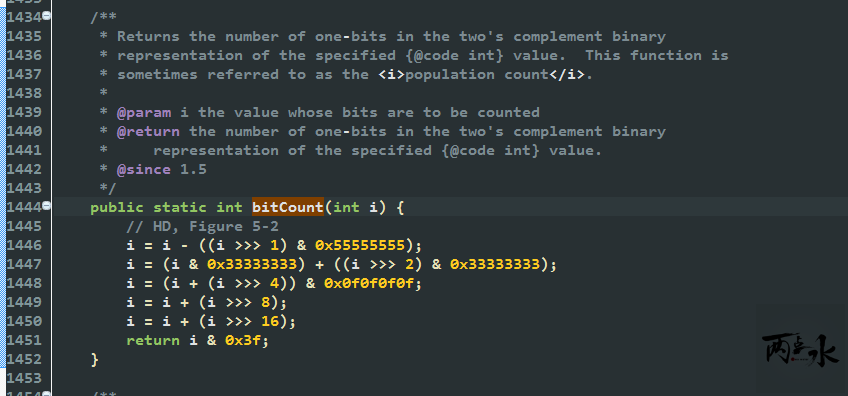
其实这个题目在 Java ,Integer 类中 bitCount 方法的已经解决了的,我们可以看下大神们是如何巧妙的解决的。
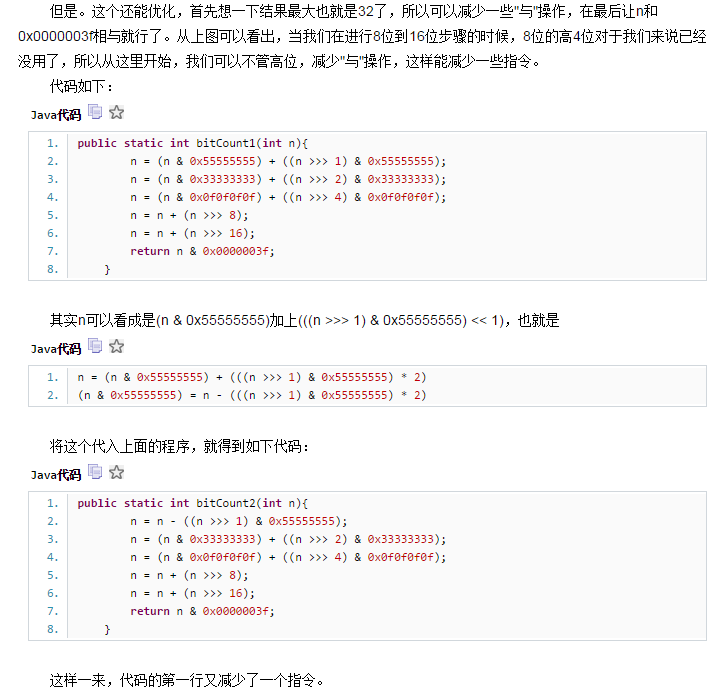
一开始没想明白怎么推出来的,最后上网查了一下,